Interior and exterior distance bounds for the Mandelbrot set
Updated September, 2022
Since these distance bounding methods are fairly complicated and non-intuitive, I found it appropriate to dedicate this appendix to them. Also, very few explanations are available on the internet (especially for the interior bound); as expected, MuEncy comments on both bounding methods, and even gives souce for the exterior bounder.
Offline, you can look up a book named "The science of fractal images", by Heinz-Otto Peitgen & Dietmar Saupe editors. This book is worth its weigh in gold.
Interior distance bounding
The first thing to remember is that the resulting distances should not be considered precise. They are only bounds; the closest point on the M border is never found. That is because of the nature of the algorithm.
What we will be doing, plain and simple, is looking for disks completely contained in M. Maybe a bigger disk would still be inside M, but that doesn't matter, because we're just calculating bounds. The algorithm relies on a theorem by Hubbard & Douady (who demonstrated that M is connected by mapping M onto the unit disk), combined with the Koebe 1/4 theorem.
The process, if I gathered correctly, is as follows:
- Map C onto the unit disk using Hubbard & Douady's method.
- Get the inverse of the map using the Möbius transformation.
- Using Hubbard & Douady's method again, we "unmap" from the inverse map to get a complex value. Its magnitude, d, will be used to compute a lower bound.
- The Koebe 1/4 theorem applies, by construction; hence, all points within a radius of d/4 from C are sure to be in M.
In practice, not only do we need C to be inside M, but we also require C's periodic cycle. That is increasingly harder to detect as C approaches the M border. The following Java snippet is an example of how to find the cycle.
/**
* Finds the periodic cycle for a given C, provided C is in M,
* and the number of iterates to check is sufficient.
* @param Cr double - Real component of C.
* @param Ci double - Imaginary component of C.
* @param maxN int - Maximum number of iterates to check.
* @return double[][] - The periodic cycle. The period equals
* 'getPeriodicCycle(Cr,Ci,maxN).length'. Returns null if C
* is outside M, and an empty array if the periodic cycle was not found.
*/
public double[][] getPeriodicCycle(double Cr, double Ci, int maxN) {
double Zr, Zi, ZrT, c1, c2;
double[] iterR = new double[maxN];
double[] iterI = new double[maxN];
int i, j, n, maxNT;
// We'll do various checks to detect more obvious cycles faster.
int[] nsToChk = new int[] { 0, 0, 0, 0, maxN };
for (i = 3; i > -1; i--) nsToChk[i] = nsToChk[i + 1] / 2;
// Start iterating.
for (n = 1, iterR[0] = Zr = iterI[0] = Zi = i = 0; i < 5; i++) {
maxNT = nsToChk[i];
while (n < maxNT) {
iterR[n] = ZrT = Zr * Zr - Zi * Zi + Cr;
iterI[n++] = Zi = 2.0 * Zr * Zi + Ci;
Zr = ZrT;
// If C is outside M, return null.
if (Zr * Zr + Zi * Zi > 4) return null;
}
// This is the periodicity check.
for (j = n - 2; j > -1; j--) {
c1 = Zr - iterR[j];
c2 = Zi - iterI[j];
if (c1 * c1 + c2 * c2 < 1E-30) {
// Okay, close enough.
int period = n - j - 1;
double[][] cycle = new double[period][2];
int offset = ((n / period) - 1) * period;
for (int k = 0; k < period; k++, offset++) {
cycle[k][0] = iterR[offset];
cycle[k][1] = iterI[offset];
}
return cycle;
}
}
}
// Iterates didn't escape, but period never became apparent
// -return empty array.
return new double[0][0];
}
Once we have the periodic cycle, the distance estimation is pretty straight-forward -see the Java source below:
/**
* Calculates a lower bound for the distance between C
* and the closest point in the border of M.
* @param cycle double[][] - C's periodic cycle.
* @return double - The interior distance estimation.
*/
public double getInteriorLowerBound(double[][] cycle) {
// Real and imaginary components for complex numbers D1, D2, D3, and D4;
// and temporary variables to store the complex numbers in recursion.
double Zr, Zi, D1r, D1i, D2r, D2i, D3r, D3i, D4r, D4i;
double D1rT, D1iT, D2rT, D2iT, D3rT, D3iT, D4rT, D4iT;
int i, period = cycle.length;
// Initial values: D1 = 1; D2 = 0; D3 = 0; D4 = 0;
D1r = 1;
D1i = D2r = D2i = D3r = D3i = D4r = D4i = 0;
// Start iterating.
for (i = 0; i < period; i++) {
// No need to iterate Z; values are already in 'cycle'.
Zr = cycle[i][0];
Zi = cycle[i][1];
// D1 = 2 * Z * D1;
D1rT = 2 * (Zr * D1r - Zi * D1i);
D1iT = 2 * (Zi * D1r + Zr * D1i);
// D2 = 2 * Z * D2 + 1;
D2rT = 2 * (Zr * D2r - Zi * D2i) + 1;
D2iT = 2 * (Zi * D2r + Zr * D2i);
// D3 = 2 * (D1^2 + Z * D3);
D3rT = 2 * ((Zr * D3r - Zi * D3i) + (D1r * D1r - D1i * D1i));
D3iT = 2 * ((Zr * D3i + Zi * D3r) + (2 * D1r * D1i));
// D4 = 2 * (D1 * D2 + Z * D4);
D4rT = 2 * ((Zr * D4r - Zi * D4i) + (D1r * D2r - D1i * D2i));
D4iT = 2 * ((Zr * D4i + Zi * D4r) + (D1r * D2i + D1i * D2r));
// Update variables.
D1r = D1rT; D1i = D1iT;
D2r = D2rT; D2i = D2iT;
D3r = D3rT; D3i = D3iT;
D4r = D4rT; D4i = D4iT;
}
// A = 1 - |D1|^2;
double A = 1 - (D1r * D1r + D1i * D1i);
// B = |D4 + D3 * (D2 / (1 - D1))|;
double B = (1 - D1r) * (1 - D1r) + D1i * D1i;
D1rT = (D2r * (1 - D1r) - D2i * D1i) / B;
D1iT = (D2i * (1 - D1r) + D2r * D1i) / B;
D2rT = D4r + (D3r * D1rT - D3i * D1iT);
D2iT = D4i + (D3i * D1rT + D3r * D1iT);
B = StrictMath.sqrt(D2rT * D2rT + D2iT * D2iT);
// Return lower bound -that is, 1/4 the estimated bound.
return A / (4.0 * B);
}
Exterior distance bounding
Computing a lower bound for the distance between a point C outside M and M is even more simple. As in the interior bounding, we rely on theorems by Hubbard & Douady, and Koebe. The actual algorithm is based on the ideas of J. Milnor and W. Thurston, expanded by A. Wilkes & J. Hubbard. Beware, though, the algorithm works well for Cs reasonably close to M.
This is the Java source:
/**
* Calculates a lower bound for the distance between C and the closest
* point in the border of M, if C is outside M.
* @param Cr double - Real component of C.
* @param Ci double - Imaginary component of C.
* @param maxN int - Maximum number of times the Mandelbrot function will be iterated.
* @return double - The approximate distance between C and the closest
* point in M. If C is in M, -1 will be returned.
*/>
public double getExteriorLowerBound(double Cr, double Ci, int maxN) {
double Zr, Zi, ZrT, ZiT, c1, c2;
double[] iterR = new double[maxN];
double[] iterI = new double[maxN];
int i, j, n, maxNT;
// We'll do various checks to detect periods faster.
int[] nsToChk = new int[] { 0, 0, 0, 0, maxN };
for (i = 3; i > -1; i--) nsToChk[i] = nsToChk[i + 1] / 2;
// Start iterating.
for (n = 1, iterR[0] = Zr = iterI[0] = Zi = i = 0; i < 5; i++) {
maxNT = nsToChk[i];
while (n < maxNT) {
iterR[n] = ZrT = Zr * Zr - Zi * Zi + Cr;
iterI[n++] = Zi = 2.0 * Zr * Zi + Ci;
Zr = ZrT;
// If C is outside M, do distance estimation.
if (Zr * Zr + Zi * Zi > 4) {
double dZr, dZi, dZrT;
int nT = n - 1;
// Recursively calculate first derivative: D = 2 * Z * D + 1;
for (dZr = dZi = i = 0; i < nT; i++) {
ZrT = iterR[i];
ZiT = iterI[i];
dZrT = 2.0 * (ZrT * dZr - ZiT * dZi) + 1;
dZi = 2.0 * (ZrT * dZi + ZiT * dZr);
dZr = dZrT;
}
// Lower bound: (2 * log |Z| * (|Z| / |D|)) / 4;
c1 = StrictMath.sqrt(Zr * Zr + Zi * Zi);
c2 = StrictMath.sqrt(dZr * dZr + dZi * dZi);
return (StrictMath.log(Zr * Zr + Zi * Zi) * c1 / c2) / 4.0;
}
}
// Periodicity check.
for (j = n - 2; j > -1; j--) {
c1 = Zr - iterR[j];
c2 = Zi - iterI[j];
if (c1 * c1 + c2 * c2 < 1E-30) return -1.0;
}
}
return -1.0;
}
Both interior and exterior bounding can be combined to produce images such as this:
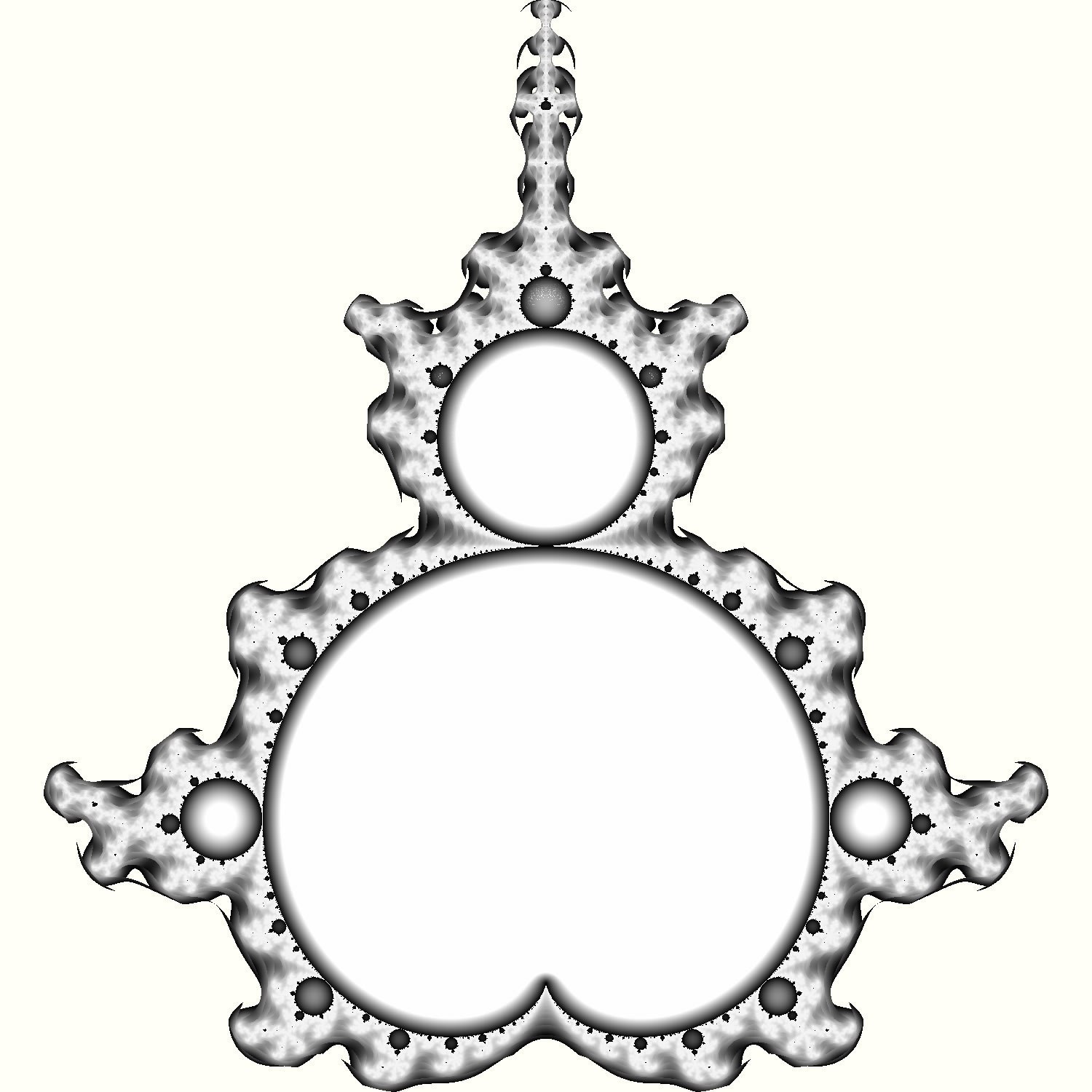
For lack of a better color palette, I used gray-scale.
Points outside M get brighter as they approach the border. Points in M get darker towards the border.
