Buddhabrot gallery

Updated September, 2022

A collection of Buddhabrot-related images and videos that I created.

The Buddhabrot's 6 major planes.

The Mandelbrot set is contained in a circle, so it can easily be turned inside out.

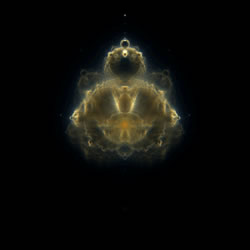
Nebulabrot render.

The Buddhabrot fits perfectly inside a 4D cube.

The formula used for the next image is Z_n = Z_n-1³ + C.

Zooming

The following images are a zoom of the '3^rd eye' on the Buddha's forehead. Each B&W image takes a color channel, and merging them all results in the last one. Center at (-1.15, 0i), width = 0.125.

Zoom of the 3^rd circumference on Buddha's head.

Center = (-1.4, 0i), width = 0.003 — center = (-1.4, 0i)
width = 0.003

The sequence below shows a deep zoom on the floating Ghostbrots on the main figure's shoulder.

Center = (-1.2025, .7075i), width = .05 — center = (-1.2025, .7075i)
width = .05

Center = (-1.21775, .70845i), width = .0008 — center = (-1.21775, .70845i)
width = .0008

Center = (-1.217963, .70835i), width = .000016 — center = (-1.217963, .70835i)
width = .000016

Center = (-1.2179607, .70834436i), width = .00000024 — center = (-1.2179607, .70834436i)
width = .00000024

The next 2 images zoom on the Buddhabrot's center. The first image shows only orbits projected by the Minibrot centerd at (-.16, 1.035i).

Center = (0, 0i), width = .3; Minibrot orbits only — center = (0, 0i)
width = .3
Minibrot orbits only

Center = (0, 0i), width = .3; all orbits — center = (0, 0i)
width = .3
All orbits

More zooms.

Center = (1.35, 0i), width = 0.125 — center = (1.35, 0i)
width = 0.125
minN-maxN red = 5 - 1000
minN-maxN green = 10 - 3500
minN-maxN blue = 15 - 6000

Center = (-0.158428, 1.03335i), width = 0.030476 — center = (-0.158428, 1.03335i)
width = 0.030476
minN-maxN red = 30 - 12000
minN-maxN green = 20 - 7000
minN-maxN blue = 10 - 2000

Center = (-1.477333, 0i), width = 0.018443 — center = (-1.477333, 0i)
width = 0.018443
minN-maxN red = 0 - 15000
minN-maxN green = 0 - 10000
minN-maxN blue = 0 - 5000

Center = (-1.25586, 0.38095i), width = 0.01054 — center = (-1.25586, 0.38095i)
width = 0.01054
minN-maxN red = 0 - 10000
minN-maxN green = 0 - 1000
minN-maxN blue = 0 - 500

Center = (0.0728025227119999, -1.1048127150340001i), width = 0.032 — center = (0.0728025227119999, -1.1048127150340001i)
width = 0.032
minN-maxN red = 20 - 10000
minN-maxN green = 20 - 15000
minN-maxN blue = 20 - 20000

Center = (-0.1915867, 0.8151886i), width = 0.0001165 — center = (-0.1915867, 0.8151886i)
width = 0.0001165
minN-maxN red = 200 - 10000
minN-maxN green = 500 - 25000
minN-maxN blue = 1000 - 50000

Animations

Rotation through the Buddhabrot's 6 major planes.

What happens as we sample more and more points on the plane? Start with 1 point per pixel, and finish with 10000.

What happens as the value of maxN increases? Start with 1, finish with 25000.

Plane sweep. Painting only trajectories that belong to points within the height 0.1 horizontal stripe.

Rotation from plane (Cr, Ci) to (Zr, Zi). This illustrates how trajectories unfold the Mandelbrot into the Buddhabrot.

Buddhagrams.

The next 3 videos show what happens when Z₀ is initialized with different values.

Zr₀ = 0, Zi₀ increases from 0:

Zr₀ increases from 0, Zi₀ increases from 0:

Zr₀ increases from 0, Zi₀ = 0:

Negative Buddhabrot

The 6 major planes, painting only trajectories that belong to points in M.

Inverted version of the previous planes.

A couple more renders.

Primitive Buddhabrot

The 6 major planes from Linas Vepstas' original idea, colored using the Buddhabrot technique.

Mutant Buddhabrots

The images below are the product of buggy code.

Buddhabrot hologram

This rendering technique uses the Mandelbrot formula, but initializes Z₀ to a random value instead of 0.

Buddhabrot hologram variations

The following images result from overlaying many axial cuttings of the 4D data -in other words, several images generated with different Z₀ values; in planes (Zr, Cr) and (Zi, Ci) the cuts are visible as diagonal lines.

The following images have been generated using different values for Z₀:

Zr0 = sqrt(abs(Cr)), Zi0 = sqrt(abs(Ci)) — Zr₀ = sqrt(abs(Cr))
Zi₀ = sqrt(abs(Ci))

Zr0 = sin(Ci), Zi0 = sin(Cr) — Zr₀ = sin(Ci), Zi₀ = sin(Cr)

Zr0 = cos(Cr), Zi0 = cos(Ci) — Zr₀ = cos(Cr), Zi₀ = cos(Ci)

Zr0 = cos(Cr), Zi0 = sin(Ci) — Zr₀ = cos(Cr), Zi₀ = sin(Ci)

Z0 = sin(complex(Ci, Cr i)) — Z₀ = sin(complex(Ci, Cr i))

Zr0 = sin(Cr), Zi0 = sin(Ci) — Zr₀ = sin(Cr), Zi₀ = sin(Ci)

Zr0 = -Cr, Zi0 = Ci — Zr₀ = -Cr, Zi₀ = Ci

Distance estimators

The image below represents the distance from each point to the closest point in the Mandelbrot set. Values outside M go brighter as they approach the border, whereas values inside M go darker as they approach the border.